terça-feira, 26 de abril de 2016
EQUAÇÃO DO 2º GRAU - APLICAÇÕES
Equações do 2° grau e suas aplicações
Não se engane, mesmo sem perceber as equações do 2º grau e a função do 2° grau estão presentes em inúmeras situações cotidianas. É claro que nós não a usamos todos os dias ou em tudo. Você não acorda num belo domingo de manhã e tem que ao escovar os dentes resolver um delta ou calcular a raiz da equação para um sorriso perfeito. Mas que as aplicações existem existem.
Como exemplo temos que,
Movimento de um projétil - Você já deve ter estado na beira de um rio ou de um lago e atirado uma pedra para o centro da água ou então jogado um objeto ou dado uma bicuda pro alto em uma bola. Note que como será a trajetória desse movimento? Uma parábola, a função do 2° grau que descreve este movimento. Olha uma equação do 2° grau ai gente !!!
Veja se a trajetória de um projétil, perceba o movimento descrito, uma parábola. A equação do segundo grau é forte presença ai. Por exemplo, para calcular a altura máxima atingida você presisa calcular o delta, para descobrir o ponto de partida e chegada é necessário resolver a equação e achar os valores de x.
Como exemplo temos que,
Movimento de um projétil - Você já deve ter estado na beira de um rio ou de um lago e atirado uma pedra para o centro da água ou então jogado um objeto ou dado uma bicuda pro alto em uma bola. Note que como será a trajetória desse movimento? Uma parábola, a função do 2° grau que descreve este movimento. Olha uma equação do 2° grau ai gente !!!
Veja se a trajetória de um projétil, perceba o movimento descrito, uma parábola. A equação do segundo grau é forte presença ai. Por exemplo, para calcular a altura máxima atingida você presisa calcular o delta, para descobrir o ponto de partida e chegada é necessário resolver a equação e achar os valores de x.
Veja também quando é arremessado uma bola de canhão ou quando atira ao centro do lago se parece com a que aparece nas seguintes simulações, uma parábola.
- na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.
Na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão
S = S0 + V0t + (at2)/2, onde a: aceleração, S: espaço, V: velocidade e t: tempo.
Olhem só: Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?
Olha uma equação do 2° grau ai gente !!!
Resolução: A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:

Olha outra aplicação na física da equação do 2° grau a Lei da Queda dos Corpos
No estudo de física a queda livre é uma particularização do movimento uniformemente variado (MRUV). Um famoso físico e astrônomo italiano chamado Galileu Galilei, introduziu o método experimental e acreditava que qualquer afirmativa só poderia ser confirmada após a realização de experimentos e a sua comprovação. No seu experimento mais famoso ele, Galileu Galilei, estando na Torre de Pisa, abandonou ao mesmo tempo esferas de mesmo peso e verificou que elas chegavam ao solo no mesmo instante.
Quando dois corpos quaisquer são abandonados, no vácuo ou no ar com resistência desprezível, da mesma altura, o tempo de queda é o mesmo para ambos, mesmo que eles possuam pesos diferentes.
O movimento de queda livre trata-se de um movimento acelerado, sofre a ação da aceleração da gravidade, aceleração essa que é representada por g e é variável para cada ponto da superfície da Terra. Porém para o estudo de Física, e desprezando a resistência do ar, seu valor é constante e aproximadamente igual a 9,8 m/s2.
As equações matemáticas que determinam o movimento de queda livre são as seguintes:
No estudo de física a queda livre é uma particularização do movimento uniformemente variado (MRUV). Um famoso físico e astrônomo italiano chamado Galileu Galilei, introduziu o método experimental e acreditava que qualquer afirmativa só poderia ser confirmada após a realização de experimentos e a sua comprovação. No seu experimento mais famoso ele, Galileu Galilei, estando na Torre de Pisa, abandonou ao mesmo tempo esferas de mesmo peso e verificou que elas chegavam ao solo no mesmo instante.
Quando dois corpos quaisquer são abandonados, no vácuo ou no ar com resistência desprezível, da mesma altura, o tempo de queda é o mesmo para ambos, mesmo que eles possuam pesos diferentes.
O movimento de queda livre trata-se de um movimento acelerado, sofre a ação da aceleração da gravidade, aceleração essa que é representada por g e é variável para cada ponto da superfície da Terra. Porém para o estudo de Física, e desprezando a resistência do ar, seu valor é constante e aproximadamente igual a 9,8 m/s2.
As equações matemáticas que determinam o movimento de queda livre são as seguintes:


nesta fórmula:
d é a distância percorrida pelo corpo até chegar ao chão;
G é a constante aceleração da gravidade;
t é o tempo que o corpo leva para chegar ao chão.
Vc consegue colocar esta fórmula, que calcula a distância em função do tempo da queda, na forma de uma equação do 2º grau? Como seria?
Saiba mais sobre os experimentos de Galileu, clique aqui.
E nas construções, na engenharia. A matemática é a base se todas as soluções da engenharia. Vc já percebeu o formato de algumas pontes e construções? Será que ela tem relação com a equação do 2° grau ou com uma parábola?
A Ponte Juscelino Kubitschek em Brasília também é uma lindíssima ponte que merece ser vista!
Está ponte ao lado (Ponte JK no DF) ao ser projetada os seus arcos arquitetônicos foram descrito através função quadrática ( três arcos logo três parábolas). Será que estes arcos podem ser descritos por meio de uma função do segundo grau?
Olha uma equação do 2° grau ai gente !!!

Se agente pensar um pouquinho mais agente descobre outras aplicações da equação de 2° grau e da função do 2° grau. Agora por favor não passe nem mais um dia sem saber para que e por que estudamos este importante e fundamental tema da matemática. Não tenha a mente pequena, amplie seus horizontes e se abra para novos conhecimentos.
Equação do 2° grau na Geometria - Dentre os conteúdos inerentes ao 9º ano do Ensino Fundamental, destacaremos cálculos envolvendo áreas e desenvolvimento de equações do 2º grau incompletas. Esses conteúdos podem ser trabalhados visando à fixação de dois importantes conteúdos em um único momento. Assim, envolve a interpretação de problemas, construção geométrica de figuras planas, elaboração e resolução de equações do 2º grau.
Exemplo 1
Um retângulo possui a medida de seu lado maior igual ao quádruplo do lado menor, e área medindo 256 m². Determine a medida de seus lados.
Equação do 2° grau na Geometria - Dentre os conteúdos inerentes ao 9º ano do Ensino Fundamental, destacaremos cálculos envolvendo áreas e desenvolvimento de equações do 2º grau incompletas. Esses conteúdos podem ser trabalhados visando à fixação de dois importantes conteúdos em um único momento. Assim, envolve a interpretação de problemas, construção geométrica de figuras planas, elaboração e resolução de equações do 2º grau.
Exemplo 1
Um retângulo possui a medida de seu lado maior igual ao quádruplo do lado menor, e área medindo 256 m². Determine a medida de seus lados.

Informe que, para calcularmos a área de uma região retangular devemos multiplicar o comprimento pela largura. Observe:

O lado de maior comprimento mede 32 metros e o de menor comprimento, 8 metros.
Exemplo 2
Um trapézio possui área medindo 384 cm². Temos que a medida da altura é o dobro da medida da base menor, e que a base maior possui a mesma medida da altura. Determine o comprimento da base maior, base menor e altura desta figura.

Área do trapézio

Lado maior: 2 * 8√2 → 16√2 cm
Lado menor: 8√2 cm
Altura: 16√2 cm
TABELA COM APLICAÇÕES MATEMÁTICAS USADAS NO DIA A DIA
Conteúdo
|
Aplicações
|
NÚMEROS POSITIVOS E NEGATIVOS
+2 -3
| Temperatura:
Usamos números positivos e negativos para marcar a temperatura.
Se a temperatura estiver em 20 graus acima de zero, podemos
representá-la por +20 (vinte positivo) . Se marcar 10 graus abaixo de
zero, essa temperatura é representada por -10 (dez negativo). Conta bancária: é comum a expressão saldo negativo. Quando retiramos (débito) um valor superior ao nosso crédito em uma conta bancária, passamos a ter saldo negativo. Nível de altitude: quando estamos acima do nível do mar, estamos em uma elevação (altitude positiva). Quando estamos abaixo do nível do mar, estamos numa depressão (altidude negativa). Fuso horário: Se a abertura de uma Copa do Mundo estiver ocorrendo às 12 horas em Londres, voce estará assistindo a essa cerimônia transmitida ao vivo, pela televisão, em horário diferente. Se você estiver em São Paulo, será às 9 horas. Em Tóquio, será às 21 horas do mesmo dia. Isso ocorre de acordo com a localização de cada cidade em relação a uma referência (nesse caso, Londres), considerada o ponto zero. |
RAZÕES E PROPORÇÕES
| Razões e proporções são utilizadas em análise de dados, pesquisas, projeções e estimativas das mudanças e transformações que poderão ocorrer no Universo. |
TRIGONOMETRIA
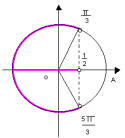 | A
trigonometria possui diversas aplicações práticas. Encontramos
aplicações da Trigonometria na Engenharia, na Mecânica, na Eletricidade,
na Acústica, na Medicina, na Astronomia e até na Música. Por exemplo, a
trigonometria do triângulo retângulo nos permite realizar facilmente
cálculos como:
|
MATRIZES
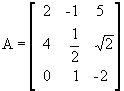 | Muitas animações que vemos no cinema utilizam matrizes. Desde o movimento dos personagens até o quadro de fundo podem ser criados por softwares que combinam pixels em formas geométricas, que são armazenadas e manipuladas. Os softwares codificam informações como posição, movimento, cor e textura de cada pixel. Para isso, utilizam vetores, matrizes e aproximações poligonais de superfícies para determinar a característica de cada pixel. Um simples quadro de um filme criado no computador tem mais de dois milhões de pixels, o que torna indispensável o uso de computadores para realizar todos os cálculos necessários. |
EQUAÇÕES
| Quando duas linhas de um mesmo plano se cruzam, obtém-se um ponto. É comum usarmos equações para indicar a localização de pessoas, barcos, aviões, cidades. |
INEQUAÇÕES
| As inequações são usadas em experiências, estatísticas, análise de dados e comparações. |
EQUAÇÕES DIFERENCIAIS
| As equações diferenciais têm ampla aplicação na resolução de problemas complexos sobre movimento, crescimento, vibrações, eletricidade e magnetismo, aerodinâmica, termodinâmica, hidrodinâmica, energia nuclear e todo tipo de fenômeno físico que envolva as taxas de variação de quantidades variáveis. |
segunda-feira, 25 de abril de 2016
terça-feira, 5 de abril de 2016
Essa é para você que odeia a matemática e a física
7 EQUAÇÕES QUE GOVERNAM O MUNDO!!!!
O alarme toca. Desligamos o despertador. São 6.30 da manhã…
Sem sair da cama temos seis equações que conduzem a nossa vida. O chip de memória que armazena a hora do relógio não poderia ter sido concebido sem uma equação fundamental da mecânica quântica. Seu tempo foi definido por um sinal de rádio que nunca teríamos sonhado de inventar, se não fosse as quatro equações de James Clerk Maxwell, as equações do eletromagnetismo. E o próprio sinal viaja de acordo com o que é conhecido como a equação de onda.
Vivemos num oceano escondido de equações. Estas estão no trabalho, nos transportes, no sistema financeiro, detecção e prevenção, na saúde e na criminalidade, na comunicação, na alimentação, na água, no aquecimento e na iluminação. Agora vai para o chuveiro e beneficia das equações utilizadas para regular o abastecimento e aquecimento da água. Os cereais do pequeno almoço vem a partir de culturas que foram criadas com a ajuda de equações estatísticas. Conduze para o trabalho e o desenho aerodinâmico do seu carro está debaixo das equações de Navier-Stokes que descrevem como o ar flui sobre e em torno da viatura. Liga o seu sistema de navegação e é envolvido pela física quântica, novamente, mais as leis de Newton do movimento e da gravidade, que ajudaram a lançar os satélites de geoposicionamento e a definir as suas órbitas. Esses satélites também usam equações geradoras de números aleatórios dos sinais de temporização, equações trigonométricas para calcular a localização, e da relatividade especial e geral para um rastreamento preciso dos movimentos dos satélites, influenciados pela gravidade da Terra.
Sem as equações, a maioria da nossa tecnologia nunca teria sido inventada. Claro, as invenções importantes como o fogo e a roda surgiram sem qualquer conhecimento matemático. No entanto, sem equações, estariamos presos num mundo medieval.
As equações vão também muito além da tecnologia. Sem elas, não teríamos conhecimento da física que rege as marés, as ondas que quebram na praia, o clima em constante mudança, os movimentos dos planetas, as fusões nucleares que ocorrem nas estrelas, as espirais das galáxias – a vastidão do universo e nosso lugar nele.
Existem milhares de equações importantes. As sete referidas aqui – a equação de onda, quatro equações de Maxwell, a transformada de Fourier e equação de Schrödinger – ilustram como as observações empíricas levaram às equações que usamos tanto na ciência como na vida cotidiana.
Equação da onda
Vivemos em um mundo repleto de ondas. Nossos ouvidos detectam sons em forma de onda, enquanto nossos olhos enxergam a luz no mesmo formato. As ondas estão em todo o lugar, da estação de rádio que sintonizamos aos abalos causados por terremotos. Mesmo assim, levamos certo tempo para poder compreendê-las.
E o que ajudou a compreender melhor o funcionamento das ondas foi a arte. Em 1727, o matemático suíço Johann Bernoulli estudou a corda de um violino e descobriu que a vibração mais simples daquela corda era uma curva de seno.
Vinte anos depois, o estudo foi revisto pelo francês Jean Le Rond d`Alembert, que focou seus cálculos na possibilidade de simplificar as equações de movimento das ondas. Com isso, ele conseguiu uma equação muito elegante e que demonstra como o formato da onda varia de acordo com o tempo, definindo sua propagação.
Uma das maiores aplicações dessa equação diz respeito ao estudo de terremotos, permitindo que sismólogos possam detectar o que está acontecendo com a Terra, centenas de quilômetros abaixo do solo.
As quatro equações de Maxwell
Mas o grande feito da equação da onda foi servir de base para os estudos sobre o magnetismo conduzidos pelo físico britânico James Clerk Maxwell. As equações criadas nesse período definem os fundamentos modernos do eletromagnetismo, aliando-o à eletricidade, ao magnetismo e à óptica.
Por volta de 1830, a maior parte dos físicos procurava alguma analogia com a gravidade para explicar os fenômenos da eletricidade e do magnetismo. Já Michael Faraday, um dos físicos mais influentes do mundo, postulava que os fenômenos elétricos e magnéticos eram causados por campos que penetravam no espaço, mudavam com o passar do tempo e podiam ser detectados pela força que eles produzem.
Em 1864, Maxwell reformulou as ideias de Faraday e escreveu quatro equações das interações básicas entre campos elétricos e magnéticos. Duas dessas equações dizem, grosso modo, que esses campos não são capazes de “escapar”, enquanto que as outras duas estipulam que, quando uma região de um campo elétrico gira na forma de um pequeno círculo, ele cria um campo magnético. Quando essas rotações acontecem em uma pequena porção de campo magnético, elas criam um campo elétrico.
Porém, a grande sacada de Maxwell veio um pouco depois, quando o cientista resolveu derivar suas equações e, por meio disso, acabou deduzindo que a luz poderia ser uma onda eletromagnética. Essa foi uma descoberta surpreendente, já que ninguém imaginava uma relação entre luz, eletricidade e magnetismo.
Segundo o cientista, a cor da luz variaria de acordo com o comprimento de onda e, com isso, Maxwell chegou à conclusão de que havia ondas longas o suficiente para serem invisíveis aos humanos. Essas ondas transformariam o mundo e ficariam conhecidas como ondas de rádio.
Em 1887, as ondas de rádio foram demostradas na prática em uma apresentação de Heinrich Hertz. Essa trajetória deu origem a uma infinidade de tecnologias, como rádio, TV, radar, celular etc.
Equações de Schrödinger
Posteriormente, os estudiosos descobriram que a luz, apesar de se comportar como uma onda, também se comportava como partículas. A partir disso, surgiu o revolucionário conceito de que a matéria é feita de ondas quânticas e que um grupo muito unido dessas ondas acaba se comportando como uma partícula.
Em 1927, o físico Erwin Schrödinger desenvolveu equações para essas ondas quânticas e, a partir delas, um novo estranho mundo surgiu: um mundo em que os elétrons, por exemplo, não eram partículas bem definidas, mas uma nuvem de probabilidades. Não demorou muito para que essas esquisitices quânticas levassem cientistas a se preocuparem com as teorias de multiversos e do famoso gato de Schrödinger.
Para quem não estuda Física, essas descobertas se materializaram em forma dos gadgets modernos, como computadores, celulares e video games. Todos esses aparelhos possuem chips de memória baseados em transistores cuja operação se dá por meio da mecânica quântica de semicondutores.
E as aplicações desses conhecimentos não param por aí, já que temos constantes exemplos de inovações realizadas com a ajuda das equações de Schrödinger. Há, por exemplo, aplicações de pontos quânticos — semicondutores muito pequeninos e que podem emitir luz de diversas cores — sendo usado em processos de imagens de material biológico, eliminando, por exemplo, o uso de corantes tóxicos. E como se não bastasse, o futuro nos promete as maravilhas do computador quântico.
Transformada de Fourier
Para finalizar, a sétima equação do artigo foi criada pelo matemático e físico francês Jean-Baptiste Joseph Fourier, que usou conceitos de ondas para explicar melhor como se dava o fluxo de calor em uma barra de metal aquecida, ou seja, como a temperatura variava ao longo do tempo. Depois de alguns anos e de muitas discussões críticas a respeito desses estudos, o mundo ganhou a versão definitiva das ideias Fourier, a sua Transformada.
Essa equação mudou a vida dos seres humanos de diversas maneiras. Para começar, com ela é possível analisar, por exemplo, o sinal produzido por um terremoto e calcular as frequências em que a energia liberada pelo tremor do solo é maior.
Além disso, a Transformada de Fourier pode ser usada para remover ruídos de gravações de áudio, encontrar a estrutura de DNAs em imagens de raio X, aperfeiçoar o recebimento de ondas de rádio e até mesmo evitar que um carro vibre mais do que o esperado. Como se não bastasse, a equação também está presente em uma das etapas de compressão usadas no formato de imagem JPG.
Não é impressionante o fato de que equações matemáticas podem ajudar a moldar o nosso mundo? Há quem diga que elas são muito mais influentes do que reis, rainhas e líderes globais, causando muito mais impacto no mundo que os governantes. Analisando os dados acima, fica mesmo difícil de não acreditar.
TUDO O QUE APRENDEMOS SOBRE A MATEMÁTICA FOI EM VÃO?
A disciplina matemática está, geralmente, ligada a inúmeros adjetivos que denotam insatisfação, medo, receio, entre muitos outros, os quais refletem de maneira significativa na vida do aluno (escolar e social). Os professores também fazem parte desse clima de descontentamento e acabam contribuindo para esse quadro de insatisfação. É importante ressaltar que alguns educadores muitas vezes preocupam-se apenas com os compromissos didáticos, cumprir todo o programa pedagógico ou realizar todas as avaliações periodicamente. Eles estão preocupados em transmitir o conhecimento escolar que é trabalhado com todo formalismo e conseqüentemente as aplicações práticas são esquecidas ou deixadas de lado. Dificilmente os exemplos dos alunos que tenham ligação com a sua vida diária são trabalhados em sala de aula, fator este que dificulta a matemática ensinada nas escolas e a sua aplicação no cotidiano.
Os melhores profissionais de todas as áreas, inclusive àquelas que não são afins, são exímios Matemáticos. Imagine você que trabalhando com Marketing digital sem saber calcular métricas de vendas, é o caminho mais rápido para o fracasso.
Tem pessoas que fazem a faculdade de Direito porque acham que não tem Matemática lá. Doce engano, pois o profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças. E se ele for tributarista então vai se ver envolvido com cálculos a vida toda. Não se engane pois em todas as profissões a Matemática está presente.
Até uma simples dona de casa usa medidores de massa (kg) em sua cozinha para fazer suas receitas. Ela nem sabe mas está sempre conectada com a Matemática.
Chegou o momento em que a humanidade percebeu que não dá pra viver sem os conhecimentos matemáticos, ou seja, a Matemática desempenha um papel de fundamental importância nos âmbitos da sociedade, desde uma simples compra de um produto, até as mais complexas situações cotidianas.
Da mesma forma que fórmulas, equações teorias e teoremas que estudamos na escola é Matemática, qualquer pensamento artístico, religioso, social, psicológico, são processos mentais matemáticos que nos acompanham desde que nascemos.
Portanto, não se iluda, no universo tudo tem base na Matemática, desde o pensamento as artes,danças Ciências , a natureza e a vida!
Os melhores profissionais de todas as áreas, inclusive àquelas que não são afins, são exímios Matemáticos. Imagine você que trabalhando com Marketing digital sem saber calcular métricas de vendas, é o caminho mais rápido para o fracasso.
Tem pessoas que fazem a faculdade de Direito porque acham que não tem Matemática lá. Doce engano, pois o profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças. E se ele for tributarista então vai se ver envolvido com cálculos a vida toda. Não se engane pois em todas as profissões a Matemática está presente.
Até uma simples dona de casa usa medidores de massa (kg) em sua cozinha para fazer suas receitas. Ela nem sabe mas está sempre conectada com a Matemática.
Chegou o momento em que a humanidade percebeu que não dá pra viver sem os conhecimentos matemáticos, ou seja, a Matemática desempenha um papel de fundamental importância nos âmbitos da sociedade, desde uma simples compra de um produto, até as mais complexas situações cotidianas.
Da mesma forma que fórmulas, equações teorias e teoremas que estudamos na escola é Matemática, qualquer pensamento artístico, religioso, social, psicológico, são processos mentais matemáticos que nos acompanham desde que nascemos.
Portanto, não se iluda, no universo tudo tem base na Matemática, desde o pensamento as artes,danças Ciências , a natureza e a vida!
Assinar:
Comentários (Atom)










